Feynman Diagrams #

Now that we have laid out the fundamentals, let’s explore Feynman diagrams by diving right in!

What is in a Feynman Diagram? #

Feynman diagrams may look like a huge jumbled mess of lines, but however complicated it may look, it only consists of lines and vertices (singular: vertex). Straight lines represent (observable) particles that are participating in the interaction, while squiggly lines represent virtual particles. Vertices occur at the intersection of lines and represent a specific point in space and time where some interesting process involving more than 1 particle occurs. Take a look at the diagram below. Can you identify the lines and vertices? How many vertices are there?

Source: Google Images

Observe that straight lines have arrows while squiggly lines do not. The arrows represent the direction in space-time that particles are travelling in.

The primitive vertex #

Now that we know what lines and vertices represent, let’s see how we can build a Feynman diagram ourselves. Here, we have the simplest building block of a Feynman diagram. This is called the primitive vertex.

Any Feynman diagram can be constructed by joining primitive vertices together, but we can’t do so randomly. There are certain rules that must be obeyed at each vertex.

Conservation of Charge #

The conservation of charge is quite logical. For instance, an up quark has a charge of $+\frac{2}{3}$, while a down quark has a charge of $-\frac{1}{3}$. This is also why neutrons, having one up quark and two down quarks is neutral, while protons, having one two up quarks and one down quark has a charge of $+1$. If a neutron ($0$) decays into a proton ($+1$), a $W^-$ boson ($-1$) must be spit out to conserve charge ($0 = 1 - 1$).

Conservation of Baryon Number #

Each baryon is given a baryon number of $1$. Since baryons are massive particles made up of 3 quarks in the standard model, quarks are given a baryon number of $\frac{1}{3}$. An antiquark, being the mathematical inverse of a quark, is hence given a baryon number of $-\frac{1}{3}$. Knowing this, what do you think the baryon number of a meson (made up of a quark and antiquark) should be?

To date, no known decay process or interaction in nature changes the net baryon number. Put another way, quarks cannot be created or destroyed in any process – if one quark enters a vertex, one quark must leave it.

Conservation of Lepton Number #

All leptons are given a lepton number of $1$, while all anti-leptons are given a lepton number of $-1$. Similar to the reasoning for conservation of baryon number, we know that if one lepton enters a vertex, exactly one lepton must leave it.

For example, an electron and anti-neutrino will balance each other out, and that’s why they appear in the beta decay of an atom.

The missing axes #

You may have recalled that we have stated earlier that vertices represent a point in space-time. That would not have been apparent yet, because we have yet to include any axes in any of the Feynman diagrams shown earlier. But now, let us try to put the final pieces in place to draw a meaningful diagram which can illustrate process. As usual, we’ll investigate this by examining a simple Feynman diagram.

Source: Google Images

In this diagram, the y-axis represents time and the x-axis represents space. Space and time are always the axes of a Feynman diagram. But how do we interpret this?

The straight line pointing in the northeast direction: An electron moves to the right as time passes. Hence, we see that as the time-coordinate increases, the space-coordinate also increases.

At the vertex (connection between the black and blue squiggly lines): The electron “collides” with a photon. This also means that they have the same position at the same time, i.e. the same space-time coordinates.

The straight line pointing in the northwest direction: After the electron encounters the photon, the photon disappears and the electron ends up moving to the left. This interaction can be described as an electron absorbing a photon.

Before we move on, we would like to remark that the x and y axes for Feynman diagrams are not fixed. Conventions differ and it is dangerous to assume the labels of the axes! What do you think will happen if you accidentally invert the axes?

Applying Transformations #

One of the fascinating things about Feynman diagrams is that if you construct a Feynman diagram for a particular particle interaction, you can duplicate, rotate, twist, flip and combine it to predict other particle interactions! Here, we shall look at a few examples.

Rotating the entire diagram #

Let’s consider a simple diagram consisting of 2 vertices:

Source: Google Images

Here, the electron starts on the left, while the positron starts on the right. Note the direction of the positron’s arrow: it is travelling backwards in time! (This is not an error. We can represent them this way because mathematically speaking, antiparticles are just the inverse of the original particle, i.e. a positron moving forward in time is equivalent to a electron travelling backwards in time. While this may seem counterintuitive, remember that time is also a dimension that we can play around with in the quantum realm.) The particles move towards each other, until a mysterious interaction happens in the middle. They are both annihilated, with two photons created at the same time. This interaction can be described as an electron-positron annihilation. Now, let’s rotate this 90$^\circ$ clockwise.

Source: Google Images

Before we try to figure out this mean, make a guess: what should the axes be?

This diagram now describes a different process. Try going through the same process described earlier. What do you think is happening here?

Twisting a vertex (in the plane of the paper) #

Some processes can be related by simply twisting (or deforming) vertices in Feynman diagrams! Here, we see an example.

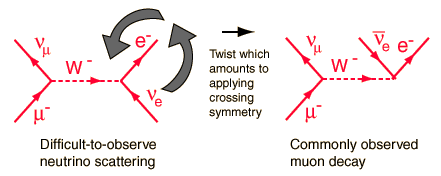
Source: http://hyperphysics.phy-astr.gsu.edu/hbase/Particles/imgpar/feynw4.gif

The exact process happening here isn’t important. Instead, what you should note is how applying this simple transformation gives us a different process altogether. In fact, this powerful feature of Feynman diagram is a visualisation of crossing-symmetry.

What is crossing-symmetry? Remember we mentioned earlier that anti particles are mathematically inverses of their regular counterparts? If we take a hypothetical process and write out the equation for it in the following form: $$ A + B \to C + D $$ Crossing-symmetry says that we can move things to the other side of the equation arrow, but we must take the inverse of it. For example, we can predict the following process from the previous one: $$ A \to \overline{B} + C + D $$ And this one too! $$ A + B + \overline{C} \to D $$ We can move multiple things as well: $$ A + \overline{C} \to \overline{B} + D $$ This holds for all known particles.

Twisting a vertex (out of the plane of the paper) #

Edited from: http://hyperphysics.phy-astr.gsu.edu/hbase/Particles/imgpar/feynx.gif

What do you think will happen if we twist a vertex this way?

What’s next? #

Now that you understand how Feynman diagrams work, read on to find out how we can apply them to explain things!